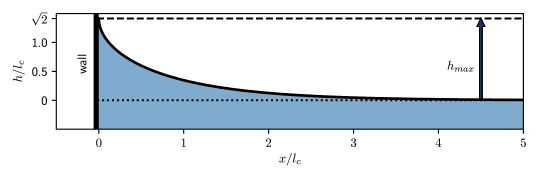
Gravity is characterized by the specific weight of the liquid $\rho g$, where $\rho$ is the liquid density and $g$ is the acceleration due to gravity. The dimensions of specific gravity are $F/L^{3}$, where $F$ denotes the dimensions of force and $L$ those of length. Since the dimensions of surface tension $\sigma$ are $F/L$, a balance of surface tension and gravity invariably yields the ratio $(\sigma/\rho g)$, which has the dimensions $L^{2}$. Based on this arises the capillary length defined as $\ell_{\text{c}}=(\sigma/\rho g)^{1/2}$. For a fluid like water, with $\sigma=72\times 10^{-3}$ N/m and $\rho g=9800$ N/m${}^{3}$, the capillary length is $\ell_{\text{c}}=2.7$ mm.